
今回は、データ構造に関する内容だね!
データ構造の仕組みや特徴について学んでいきましょう!
本記事で学べること
・基本的なデータ構造の仕組み・特徴
はじめに
データ構造には、さまざまな種類があり、それぞれのデータ構造には、長所と短所があるため、プログラムの要件に応じて適切なデータ構造を選択する必要があります。本記事では、さまざまなデータ構造の特徴を紹介することで、読者の選択肢を増やすと共に、選択するための判断基準を提供したいと考えています。
それでは本題に入りましょう。まず、データ構造とは何かについて説明したいと思います。
データ構造とは
データ構造とは、データの集合を目的に応じて特定の形式で格納および管理するために使われる、形式化されたデータ構成のことをいいます。データ構造は、データの効率的な検索、追加、削除、更新などを可能にすることで、プログラムのパフォーマンスを向上させます。
データ構造の選択は、プログラムのパフォーマンスに大きな影響を与えます。適切なデータ構造を選択することで、プログラムの実行速度を向上させ、メモリ使用量を削減することができます。また、データ構造の選択は、プログラムの保守性にも影響を与えます。適切なデータ構造を選択することで、プログラムのコードがわかりやすく、変更が容易になります。
さっそく具体的なデータ構造について紹介していきましょう。
リスト
リストは、複数の要素を順序付けて格納するためのデータ構造です。それでは3つのデータからなるリストを例にして、詳しく説明していきましょう。

リストでは基本的に、一つのノードにデータと次のノードを指すポインタが含まれています。今回は、前二つのノードに、Apple とポインタ、Peach とポインタがそれぞれ格納されています。ただし、Lemon が格納されているノードは、ポインタが格納されないことに注意してください。これは、Lemon が格納されているノードが最後尾であるため、その先にアクセスするノードがないからです。
各ノードには、ポインタを頭から辿ることでしかアクセスできません。この例の場合、Lemon にアクセスしたいときには、まず Apple にアクセスし、さらに Peach を辿らなければなりません。
データの追加は、追加する前後のポインタを指し替えるだけで済むので、簡単に行えます。例えば、Peach と Lemon の間に Mango を追加したいときには、Peach のポインタを Mango に指し替え、Mango のポインタを Lemon に向ければ完了です。
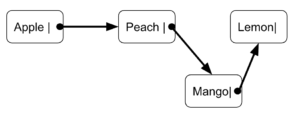
データの削除も追加のときと同様に、ポインタの指し替えで行えます。例えば、Mango を削除したかったら、Peach のポインタを Lemon を指すようにすればいいだけです。
以上をまとめると、リストには、データの追加や削除がしやすい反面、アクセスには時間がかかるという特徴があります。なお、ここでは、最も基本的な単方向リストの仕組みについて説明しましたが、他にも最後尾のノードが先頭のノードを指す環状リストや各ノードにポインタを二つ持たせて前後のノードを指すようにした双方向リストなどがあります。
配列
配列は、データを一列に並べます。a という名前の配列に3つのデータが格納されているとすると、a の横の [ ] は、配列の何番目かを表しています。
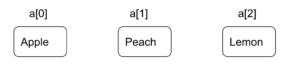
配列では、インデックスを指定するだけで、求めているデータに直接アクセスすることができます。Lemon にアクセスしたいときは、a[2] を指定すれば直接アクセスできます。
データを追加する場合は、リストに比べてコストが高くなります。例を使って説明すると、a[1] に Mango を追加する場合、まず、配列の最後に追加する空間を確保します。
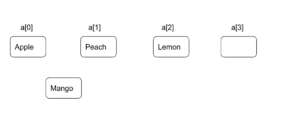
その後、追加される空間を空けるため、1つずつデータをずらしていきます。つまり、まず Lemon をずらし、その後に Peach をずらすことになります。そして、Mango を a[1] に格納します。
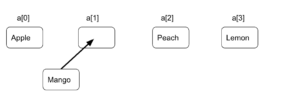
データを削除する場合は、追加と逆の手順を踏めばよいです。つまり、Mango を削除する場合、まず、Mango を削除し、その後で、Peach、Lemon を右に一つずつずらします。
配列には、データへのアクセスは簡単に行えますが、追加や削除にコストがかかるという特徴があります。
スタック
スタックは、LIFO(Last In, First Out, 後入れ先出し)の原則に則ったデータ構造です。後に追加したデータほど、先に取り出します。なおスタックでは、データを追加することをプッシュ、データを取り出すことをポップといいます。
例えば、Apple というデータをプッシュし、その後で Peach というデータをプッシュした場合、以下のようになります。
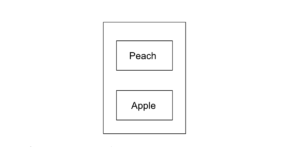
ここでポップを行うと、Peach が取り出されます。
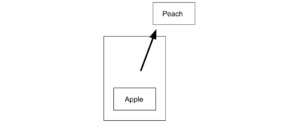
スタックは、途中のデータにはアクセスできませんが、常に最新のデータにアクセスしたいときには便利です。
キュー
キューは、FIFO(First In, First Out, 先入れ先出し)の原則に則ったデータ構造です。先に追加したデータほど、先に取り出します。なおキューでは、データを追加することをエンキュー、データを取り出すことをデキューといいます。
例えば、Apple というデータをエンキューし、その後で Peach というデータをエンキューした場合、以下のようになります。
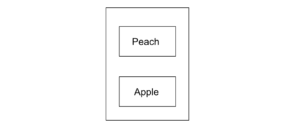
ここまでは、スタックと同じですね。しかし、ここで、デキューした場合、Apple が取り出されます。
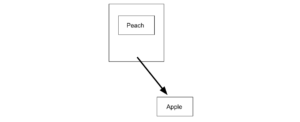
キューは、スタックと同様に、途中のデータにはアクセスできません。しかし、常に古いデータから処理したいときには便利です。
ハッシュテーブル
ハッシュテーブルは、ハッシュ関数を利用することで、キーとバリューがセットになったデータの検索を効率的に行えるようにしたデータ構造です。例えば、[キー, バリュー] が [太郎, 男] のデータを 5 つの箱がある配列に格納することを考えてみましょう。

まず、キーである太郎をハッシュ関数で変換します。すると、3569 になったとします(なお、ハッシュ関数の出力結果をハッシュ値と呼びます)。
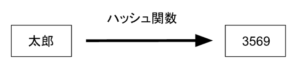
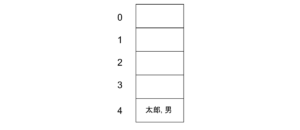
これを mod 5( 5 つの箱がある配列を考えているため)で考えると、3569 は 4 に等しくなります。したがって、[太郎, 男] は、4 の箱に格納されることになります。
次に、[ 花子, 女] というデータを考えてみましょう。花子をハッシュ関数で格納して、mod 5 で考えたときに、結果が 0 ~ 3 のどれかと等しくなった場合、等しくなった番号の箱に格納します。もし、結果が 4 と等しくなった場合、以下のようにリストを利用して、[太郎, 男] のデータにつなげます。
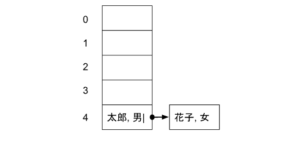
ハッシュテーブルは、ハッシュ関数を利用することで、データへの素早いアクセスを可能にしています。また、ハッシュ値を mod 演算した結果が衝突した時には、リストを利用します。また、今回紹介したリストを利用する方法は、チェイン(連鎖)法と呼ばれており、他にもハッシュ関数をいくつか利用する方法や線形操作法などがあります。
ヒープ
ヒープは、グラフの木構造の一種で、プライオリティキューの実装のときに使われます。プライオリティキューとは、データを自由に追加でき、小さいものから取り出すことができるデータ構造です。例として、以下のヒープについて考えてみましょう。各ノードに書かれている数字が格納されているデータです。
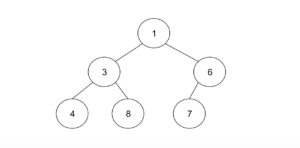
ヒープは、最大2つの子ノードを持ち、ノードは上に詰め、同じ段では左に詰めます。また、子ノードの数字は必ず親ノードの数字よりも大きくなります。
ここで、ヒープに5を追加してみましょう。初めは、6の右側の子ノードに格納されますが、それだと親ノードの方が子ノードよりも大きくなってしまうので、5の位置と6の位置を入れ替えます。
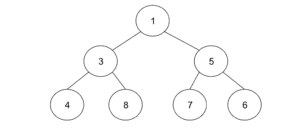
次に、ここから1を削除する場合を考えてみましょう。1を削除した場合、最後尾の数が1に移動します。ヒープは上詰め、左詰めなので、今回は、6になります。
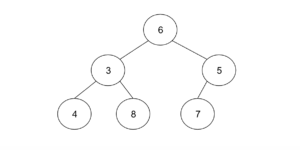
しかし、このままだと、親ノードが子ノードより大きくなるので、子ノードのうち小さい方と入れ替えます。3と5だと3の方が小さいので、3と6を入れ替えます。
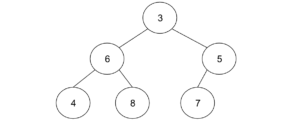
同様に、6と4を入れ替えれば完成です。
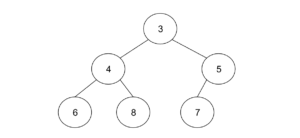
ヒープは、常に一番上に最小のデータがあるため、最小値を取得しやすいという特徴があります。
2分探索木
2分探索木は、グラフの木構造を利用したデータ構造です。各ノードは最大2つの子ノードを持ちます。以下の例を使って、説明していきます。
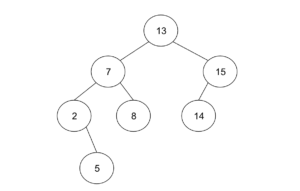
2分探索木は、全てのノードは、そのノードの左部分木に含まれる数よりも大きくなければいけないという特徴があります。例えば、13はその左部分木に含まれる、7, 2, 8, 5よりも大きくなっています。また、全てのノードは、そのノードの右部分木に含まれる数よりも小さくなくてはいけません。例えば、7は8よりも小さくなっています。この2つの特徴から、2分探索木に格納されたデータの最小値は、決まって左部分木を辿った末路にあります。今回の場合は、2が最小値となります。
それでは、2分探索木にデータを追加してみましょう。4を追加してみることにしましょう。まず、4と13を比べると、4の方が大きいので、左に一段下がります。次に、7と比べると、7の方が大きいので、左に一段下がります。そして、2と比べると4の方が大きいので、右に一段下がります。最後に5と比べると5の方が大きいので、4は5の左側の子ノードに位置することになります。
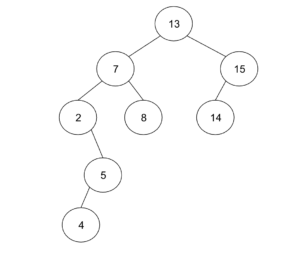
次に、2分探索木からデータを削除してみることにします。7を削除してみましょう。このとき、7の左部分木から最大ノードを見つけ、7の位置に移します。今回は、5を移します。5を移した後は、4を5の位置に移して完成です。

2分探索木では、前述した2つの特徴を持つため、データの探索を行う際には、現在いる場所のデータとの大小を比較するだけで右と左のどちらに進めばよいのかが簡単にわかるようになっています。なお、2分探索木では一つのノードが持つ子ノードの数は最大二つまでですが、この制約を3つ、4つ・・・と拡張した木構造のことをB木と呼びます。
まとめ
今回は、プログラムに関わる人なら絶対に知っておきたい重要な7つのデータ構造について紹介しました。データ構造について初めて学ぶ人にとっては少々難しく感じたかもしれませんが、本記事の内容を丁寧に追っていけば、必ず理解できると思います。根気強く頑張りましょう!
各種お問い合わせ




